Statistiek

De Statistische Analyse van een Steekproef van gemeten gegevens wordt in volgende drie fasen uitgevoerd :

Beschrijving van de Steekproef.

In deze fase tracht men een goed inzicht te bekomen in de karakteristieken van de steekproef.
Daartoe wordt de Steekproef op volgende manieren beschreven:
- Beschrijving van de meetperiode
  - Aantal metingen verspreid over de meetperiode
    
    Grafische voorstelling
  - Representatieve meetperiode
    
    Hierbij wordt door correlatie in de tijd een tijdsinterval DT bepaald waarbinnen een meting representatief is. Door rond ieder meetpunt deze DT te plaatsen kan men de totale periode berekenen waarover men representatieve resultaten heeft.
- Frequentie van voorkomen met indeling in klassen
  
  De gemeten waarden worden ingedeeld in klassen. Binnen iedere klasse wordt berekend hoeveel % van de gegevens erin voorkomen. Dit is de frequentie van voorkomen.
  In formulevorm geeft dit :
      - N : totale aantal metingen.
      - n_k : aantal metingen in de klasse k.
      - FV(k) : frequentie van voorkomen in de klasse k.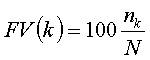
  
  De overschrijdingsfrequentie wordt als volgt bepaald :
  Beschouwt men de klasse k, die begrensd wordt door :
          w_kl < w < w_kh     (met w_kl en w_kh de onder en bovengrens van de klasse k)
  Met K het totale aantal klassen wordt w_kl, zijnde de ondergrens van de klasse k,
  n_k+n_k+1+...+n_K maal overschreden.
  De overschrijdingsfrequentie OF(k) is de procentuele uitdrukking van het totaal aantal waarden w > w_kl :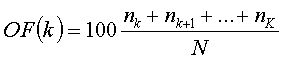
  
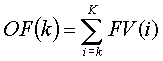
  Voor sommige hydrometeo-data (golfhoogte, windkracht) wordt een bijkomende klasse-ingedeeld gemaakt volgens de richting (golfrichting, windrichting) die op hetzelfde ogenblik van de meting gold. De richting wordt daarbij ingedeeld in sectoren (index j) . Wanneer Ns simultane metingen bestaan van de hoofdparameter en de richtingsparameter, dan wordt de frequentie van voorkomen FV(jk) gegeven door :
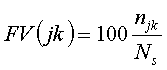
- Steekproefkarakteristieken
  
  Volgende karakteristieken van de steekproef worden berekend (x_i zijnde de waarnemingen) :
  - het gemiddelde m :
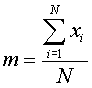
  - de standaard afwijking s en variantie s² welke een maat voor de spreiding geeft :
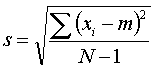
  - de percentielen geven de waarde voor dewelke x procent van de metingen kleiner zijn : bijvoorbeeld het 90% percentiel is de waarde waarbij 90% van de waarnemingen kleiner zijn dan deze waarde.
  De evolutie van deze karakteristieken door de jaren wordt getoond in een Grafische voorstelling.
  
  Om de seizoensinvloed te bestuderen worden de gegevens ook opgesplitst in de maanden van het jaar en grafisch voorgesteld
  
  De steekproefkarakteristieken per richting worden op de volgende tabelvorm en grafische manier voorgesteld.
- Correlatie met een andere parameter
  
  Om de graad van overeenkomst of correlatie met een andere parameter na te gaan wordt de lineaire regressie, met volgende grootheden, berekend :
  - De covariantie s_xy :
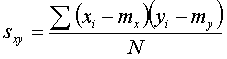
  - De correlatiecoefficient r geeft de mate van verband met de andere parameter (0=geen verband, 1=absoluut positief verband, -1=absoluut tegengesteld verband) :
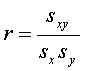
  - Deze correlatiecoefficient kan getoetst worden tegen een r_min welke afhankelijk is van het aantal waarnemingen. Bij r > r_min wordt een correlatie of verband tussen de twee parameters verondersteld.
  - De regressielijn geeft het verband kwantitatief weer, zodat op grond van een bekende waarde van x de bijbehorende waarde van y kan worden afgeleid. Deze lijn gaat door het punt (m_x,m_y) en wordt weergegeven door de volgende regressieformule :
    
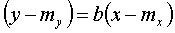
    Daarbij is b de regressiecoefficient van de steekproef :
    
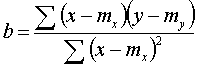
    Omgekeerd geeft volgende regressielijn de waarde van x in functie van y :
    
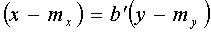
    Bij beide rechten wordt een 95% betrouwbaarheidsinterval gegeven.
    Hoe beter de correlatie tussen de twee parameters hoe kleiner de hoek tussen de twee lijnen.
    
    Soms is de correlatie complexer en volstaat de lineaire regressie niet. Bijkomend onderzoek is dan noodzakelijk. Zie hiervoor de nota Relaties tussen de parameters in de HydroMeteoAtlas
  Deze eerste fase resulteert in de keuze van de distributiefunctie die het best past bij het karakter van de steekproef en het domein waarin men de verdere analyse wil gebruiken. Bijvoorbeeld de bestudering van de hoogste waarden zal een extreme waardendistributie (vb Weibull-distributie) verantwoorden.
- Schatting van de parameters van de distributiefunctie
  
  Elke distributiefunctie bevat een aantal parameters die toelaten om de functie zo dicht mogelijk de waargenomen metingen in de steekproef te doen benaderen. Om deze parameters te bepalen kan men volgende methodes hanteren :
  - Momentenmethode
    
    Bij de momentenmethode worden de steekproefmomenten (gemiddelde, de variantie, ...) gelijk gesteld aan de corresponderende momenten van de theoretische distributie.
  - Maximum Waarschijnlijkheidsmethode
    
    De methode van de maximum kans bestaat erin als schattingen van de parameters van de distributie die waarden te nemen die de kansfunctie maximaal maken.
  - Methode van de Kleinste Kwadraten
    
    De schatting van de parameters wordt bekomen door het minimum te bepalen van de som van de kwadraten van de afwijkingen van de steekproefwaarden ten opzichte van hun theoretische waarde.
- Verificatie van het model
  
  Daarbij wordt de overeenkomst onderzocht tussen de theoretische distributie en het empirisch materiaal.
  
  Deze verificatie kan als volgt gebeuren :
  - Visuele controle
    - Q-Q plot
      
      Hierbij worden op waarschijnlijkheidspapier (De assen zijn aangepast aan de distributiefunctie zodanig dat die een rechte voorstelt) het Histogram met indeling in klassen van de Cummulatieve distributie getekend.
      De waarden van het histogram moeten zo dicht mogelijk bij de rechte van de distributiefunctie liggen.
      
      In de plaats van een histogram met klasseindeling kan men ook op waarschijnlijkheidspapier alle metingen uitgezet met als abcis de waarde en als ordinaat de orde-statistiek (i-0.5)/N. (i is hierbij het nr van de metingen na sorteren van de steekproefverzameling, N is het aantal metingen)
      Ook hier moeten de punten van de metingen moeten zo dicht mogelijk bij de rechte van de distributiefunctie liggen.
      
      Grafische Voorstelling
    - Gefitte waarde in functie van geobserveerde waarde.
      
      In grafiek wordt de gefitte orde-statistiek uitgezet in functie van de orde-statistiek van de waarden.
      Bij een goede fit moet deze lijn dicht bij de rechte y=x liggen.
      
      Grafische Voorstelling
  - Statistisch testen
    
    Via diverse statistische methodes (vb de Bootstrapmethode) wordt de Goodness-of-fit nagegaan. Dit geeft een beoordeling hoe goed de theoretische distributie met haar gekozen parameters de steekproef benaderd.